Sphere
이번엔 구다. 지금까지는 일반적인 xyz 좌표로 점을 찍었지만, 구는 구면 좌표계를 통해 찍어야 한다.
일단 극좌표 부터 이해를 하자.
극좌표
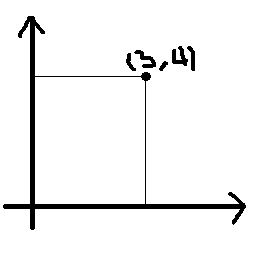
이 좌표에서 극좌표는
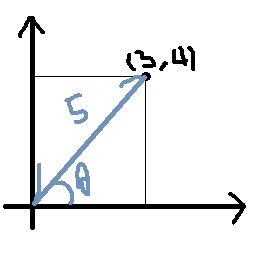
이렇게 각도와 길이가 주어졌을 때 (5,θ) 로 표현이 가능하다.
그런데 어떻게 저 좌표로 구현이 가능할까?
cosθ = 3/5 이기 때문에 θ = cos^-1(3/5) 이렇게 치환이 가능하다.
따라서 (5,cos^-1(3/5))로 구할 수 있다.
거리가 5인 점들은 많지만, x축을 기준으로 했을때 각도가 θ인 좌표는 저기 뿐이기 때문이다.
원주좌표
설명은 Directx의 Y좌표가 Z 좌표로 하고 설명한다.
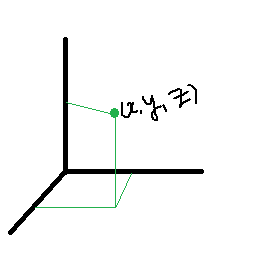
이 좌표가 흔하게 사용하는 좌표다
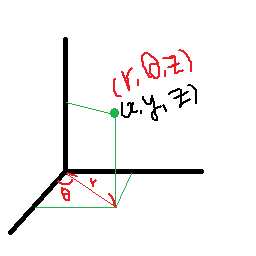
이렇게 위에서 배운 극좌표를 이용하면 이런 식으로 좌표를 구할 수 있다.
이렇게 하면 각 점들을 일반 좌표보다 빠른 속도로 구할 수 있다.
구면좌표
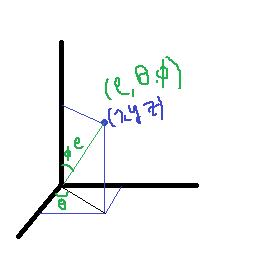
여기서 중요한 점이 있는데 θ는 상관 없지만, Φ의 경우에는 z축의 양의 방향으로부터의 각도
그러니까 항상 0 <= Φ <= π 이 범위를 갖는다.
z축의 좌표는 e * cos(Φ)
x축의 좌표는 e * sin(Φ) cosθ 가 된다.
y축의 좌표는 r * sin(θ) 이기 때문에 r 은 e * sin(Φ) 그러니 e * sin(Φ)* sin(θ)가 된다.
e은 직교 좌표계에서 √(x^2 * y^2 * z^2) = e 이기 때문에 e^2 = x^2 * y^2 * z^2 이 된다.
구를 그릴땐 마지막에 구면좌표를 이용해서 그린다.
MeshSphere.cpp
void MeshSphere::Create()
{
vector<MeshVertex> v;
v.push_back(MeshVertex(0, radius, 0, 0, 0,0, 1, 0));
float phiStep = Math::PI / stackCount;
float thetaStep = Math::PI * 2.0f / sliceCount;
for (UINT i = 1; i <= stackCount - 1; i++)
{
float phi = i * phiStep;
for (UINT k = 0; k <= sliceCount; k++)
{
float theta = k * thetaStep;
Vector3 p = Vector3
(
(radius * sinf(phi) * cosf(theta)),
(radius * cosf(phi)),
(radius * sinf(phi) * sinf(theta))
);
Vector3 n;
D3DXVec3Normalize(&n, &p);
Vector2 uv = Vector2(theta / (Math::PI * 2), phi / Math::PI);
v.push_back(MeshVertex(p.x, p.y, p.z, uv.x, uv.y, n.x, n.y, n.z));
}
}
v.push_back(MeshVertex(0, -radius, 0, 0, 0, 0, -1, 0));
vertices = new MeshVertex[v.size()];
vertexCount = v.size();
copy(v.begin(), v.end(), stdext::checked_array_iterator<MeshVertex *>(vertices, vertexCount));
vector<UINT> i;
for (UINT k = 1; k <= sliceCount; k++)
{
i.push_back(0);
i.push_back(k + 1);
i.push_back(k);
}
UINT baseIndex = 1;
UINT ringVertexCount = sliceCount + 1;
for (UINT k = 0; k < stackCount - 2; k++)
{
for (UINT j = 0; j < sliceCount; j++)
{
i.push_back(baseIndex + k * ringVertexCount + j);
i.push_back(baseIndex + k * ringVertexCount + j + 1);
i.push_back(baseIndex + (k + 1) * ringVertexCount + j);
i.push_back(baseIndex + (k + 1) * ringVertexCount + j);
i.push_back(baseIndex + k * ringVertexCount + j + 1);
i.push_back(baseIndex + (k + 1) * ringVertexCount + j + 1);
}
}
UINT southPoleIndex = v.size() - 1;
baseIndex = southPoleIndex - ringVertexCount;
for (UINT k = 0; k < sliceCount; k++)
{
i.push_back(southPoleIndex);
i.push_back(baseIndex + k);
i.push_back(baseIndex + k + 1);
}
indices = new UINT[i.size()];
indexCount = i.size();
copy(i.begin(), i.end(), stdext::checked_array_iterator<UINT *>(indices, indexCount));
}
굉장히 많다…. 하나하나 차근차근 보자
맨 위와 아랫점은 반복문이 아니고 따로 설정하고,
한번에 스텝마다 각 축들을 원으로 그리면서 하나하나 찍는다. 한 줄을 다 찍었다면 다음엔 한칸 내려서 또 그린다.
이런 방법으로 쭉 정점을 찍고
IndexBuffer의 경우에는 사각형 찍는 방향과 동일한 방향으로 찍어준다.
이렇게 하면
이렇게 원으로 잘 나온다.
이걸 wireframe으로 보면
이렇게 수많은 삼각형으로 이뤄졌다.

